Galileo and Experimental Philosophy
Greg Dawes writes…
In a recent conference paper I have argued that in some key respects Galileo’s natural philosophy anticipates the experimental philosophy of the later seventeenth century. I am not claiming that Galileo uses the term “experimental philosophy.” Nor do I claim that he makes any distinction comparable to that between experimental and speculative natural philosophy. His Italian followers in the Accademia del Cimento would later do so, but he does not. Nonetheless, the way in which Galileo undertakes natural philosophy displays at least two of the features that Peter Anstey and his collaborators have argued are characteristic of experimental philosophy.
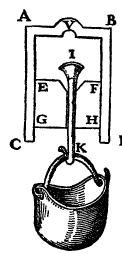
Galileo's sketch of a device to demonstrate the power of a vacuum.
The first of these has to do with the role of experiment. Much of the twentieth-century debate centred on whether Galileo actually performed the experiments about which he writes. But the more important question has to do with the role of experiments in Galileo’s thought. Like his Aristotelian predecessors, Galileo seeks to construct a demonstrative natural philosophy: one in which the conclusions follow with certainty from the premises. But unlike the Aristotelian, he relies on geometrical proofs. Like any mathematical proofs, these can be elaborated in an a priori fashion, without any reference to experience. But whether a particular proof applies to the world of experience – or, better still, whether it accurately describes the structure of the world – can only be ascertained experimentally. It is experiment which tells us which geometrical proof is to be used, even if the geometrical proof itself can be developed independently of experience. (I am relying here on the work of Martha Féher, Peter Machamer, and others.)
Perhaps more importantly, Stephen Gaukroger has argued that experimentation shaped the very way in which Galileo’s physical theories are framed and formulated. Alexander Koyré and others have argued that the laws of Galilean physics are “abstract” laws which refer to an ideal reality. It is true, of course, that in setting aside “impediments” (impedimenti), such as the resistance of the air, Galileo’s proofs do not refer to the world of everyday experience. But it is unhelpful to think of them as an idealisations of, or abstractions from, experienced reality. There is an experienced reality to which they conform. It may not be that of everyday experience, but it is that of carefully controlled physical experiments. It follows that in Galileo’s work, the task of natural philosophy is being rethought. It is no longer the study of reality as revealed to everyday observation; it is the study of that reality revealed in experimental situations.
The second way in which Galileo’s natural philosophy anticipates the later experimental philosophy is in its comparative lack of interest in the mechanisms thought to underlie phenomena. It is not that Galileo was a positivist in our modern sense. There are passages in which he engages in speculation regarding matter theory and on these occasions he favours a corpuscularian view. But such speculations are, as Salviati says in the Two New Sciences, a mere “digression.” Galileo does not consider that his new science requires them. Indeed his work on motion is almost entirely a kinematics – as he freely admits, it says nothing about the causes of motion – but Galileo does not consider it any less significant as a result.
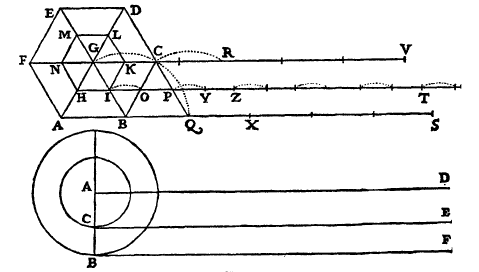
Galileo's solution of the "rota Aristotelis" paradox, demonstrating that a body could be composed of an infinite number of unquantifiable atoms.
This should not be interpreted as a general lack of interest in causation, as Stillman Drake suggests. Galileo shares the ancient desire cognoscere rerum causas (to know the causes of things). But the causal properties Galileo seeks are different from those sought by his predecessors. His causes are the mathematically describable properties of the objects whose behaviour is being explained, properties that no Aristotelian would regard as essential. (Even his atoms are more akin to mathematical points than physical objects.) It is, once again, experimentation that allows us to pick up which of those mathematically describable properties are generally operative and therefore the proper subject of a science. It is this move that allows Galileo, as it would later allow Newton, to be content with a causal account that remains on the level of phenomena, rather than speculating about a realm inaccessible to observation.
In an early dialogue, Galileo has two rustics (contadini) speculating about the new star of 1605. One of them advises his companion to listen to the mathematicians rather than the philosophers, for they can measure the sky the way he himself can measure a field. It doesn’t matter of what material the heavens are made. “If the sky were made of polenta,” he says, “couldn’t they still see it alright?” This is surely something new in the history of natural philosophy.
Postscript:
While I would still defend the individual claims contained here, my continued study of Galileo has made me increasingly cautious about the usefulness of a distinction between experimental and speculative natural philosophy. It is certainly the case that many late seventeenth-century thinkers made such a distinction, but is it a useful one for us to make? I’m not confident that it is.
Experiment certainly played an important role in Galileo’s work, although precisely what that role was continues to be contested. And it is true that Galileo has little interest in speculating about the underlying structure of the world: even if, as he writes, the sky were made of polenta, the mathematicians could still measure it. The problem is that the classical, mathematical tradition out of which he comes — that of astronomy, statics, optics, and (after Galileo) the study of local motion — cannot be helpfully characterized as either experimental or speculative. It certainly uses experiment, but it also reasons a priori, in ways that seem independent of experience.
So perhaps it would be better to have a threefold classification of early modern scientific traditions. (A classification of this kind is suggested by Casper Hakfoort in the last chapter of his Optics in the Age of Euler.) A first tradition would be that of matter theory, which is inevitably speculative insofar as it deals with matters not accessible to direct observation. (This is the realm of Newton’s “hypotheses.”) Corpuscularian proposals would fall into this category, as would Descartes’s vortex theory. A second tradition would be that of experimental natural philosophy, which regarded the results of experiment as themselves significant forms of knowledge, whether or not they could be connected with an underlying theory of the nature of matter. Finally, there is the mathematical tradition that Galileo transformed, so successfully, by producing a mathematical account of local motion.
Individual natural philosophers could engage in all three kinds of activities, but will differ according to the emphasis they place on one or other of them. So although Galileo certainly engaged in experiments, his emphasis was on the kind of reasoning characteristic of the mathematical tradition. It is this form of reasoning, I have come to believe, that cannot be easily fitted into the experimental-speculative scheme.

